近日,浙江大学上海高等研究院常务副院长吴飞教授和况琨老师团队在因果推断领域取得了新突破。针对因果推断中混淆因素未知等挑战,有效利用工具变量是一种有效方法。诺贝尔经济学奖2021年授予美国伯克利加州大学经济学教授戴维·卡德(David Card)、麻省理工学院经济学教授约书亚·D.安格里斯特(Joshua D.Angrist)以及和斯坦福大学经济学教授奎多·W.因本斯(Guido W.Imbens),以表彰他们在现代经济学中所引发的因果推断革命。
经济学家将随机实验应用到研究经济社会问题中,比如对接种疫苗选择某些区域提供补助和激励机制,再与那些维持现状的区域进行对比来看相关机制对疫苗接种率的影响。但是在很多经济学的问题上,不一定有条件做完全的随机试验。这个时候就需要凭借现有的数据来评估已经发生的事情,构建一个自然实验——通过观测到的数据,而不是去做田野实验收集的数据来进行因果推断。安格里斯特和因本斯的研究表明,使用工具变量(instrumental variable,IV),即与是否受到干预相关而与其他影响结果的因素无关的变量,可以识别出针对依从实验或准实验分配的个体(compliers to the assigned treatment)的局部平均干预效应。
传统工具变量方法依赖于提前定义好的工具变量,而在现实应用中,很难找到满足条件的工具变量。在上海人工智能创新中心和繁星科学基金支持下,团队通过机器学习赋能因果推断,先后攻克了非线性工具变量回归、工具变量发现和生成等难点问题,提出了基于混杂因素平衡的工具变量回归算法、基于无效工具变量的因果推断模型和表征学习自动生成工具变量的因果推断框架,并开源开放了基于工具变量的大数据因果推断框架。
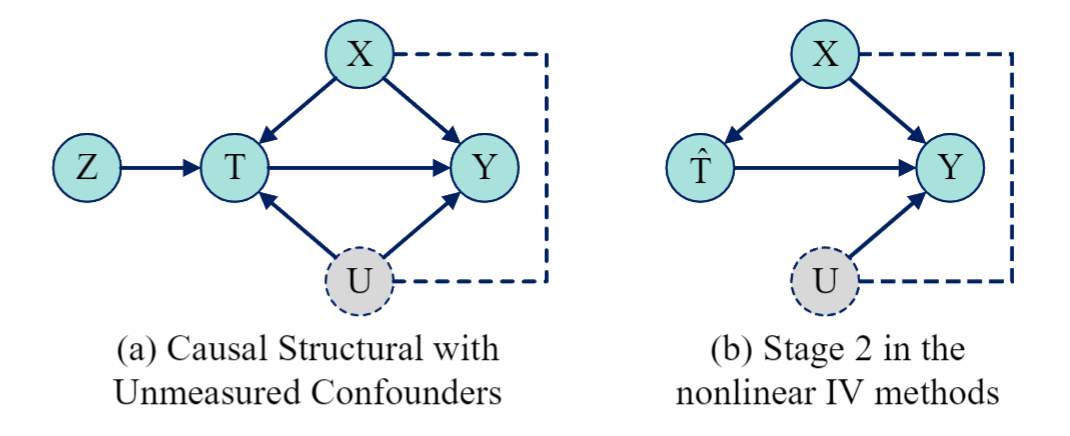
基于混杂因素平衡的工具变量回归[1]主要考虑了在存在未测量的混杂因素的情况下从观察数据中估计治疗效果这一挑战。传统方法是利用工具变量(IV)进行两阶段回归,但这类方法仅限于线性情况。最近,许多非线性IV回归的变体被提出来,其在第一阶段用IV和观察到的混杂因素对治疗进行回归,但会往往导致第二阶段观察到的混杂因素的不平衡问题。为了解决该问题,我们提出了一种混杂因素平衡的IV回归(CB-IV)算法,以共同消除未测量的混杂物的偏差并平衡观察到的混杂物。该方法第一次实现了在IV回归中结合混杂因素平衡进行治疗效果估计。在理论上,这一研究重新定义并解决了潜在结果函数的估计逆问题。实验表明,该方法优于现有的因果推断方法。
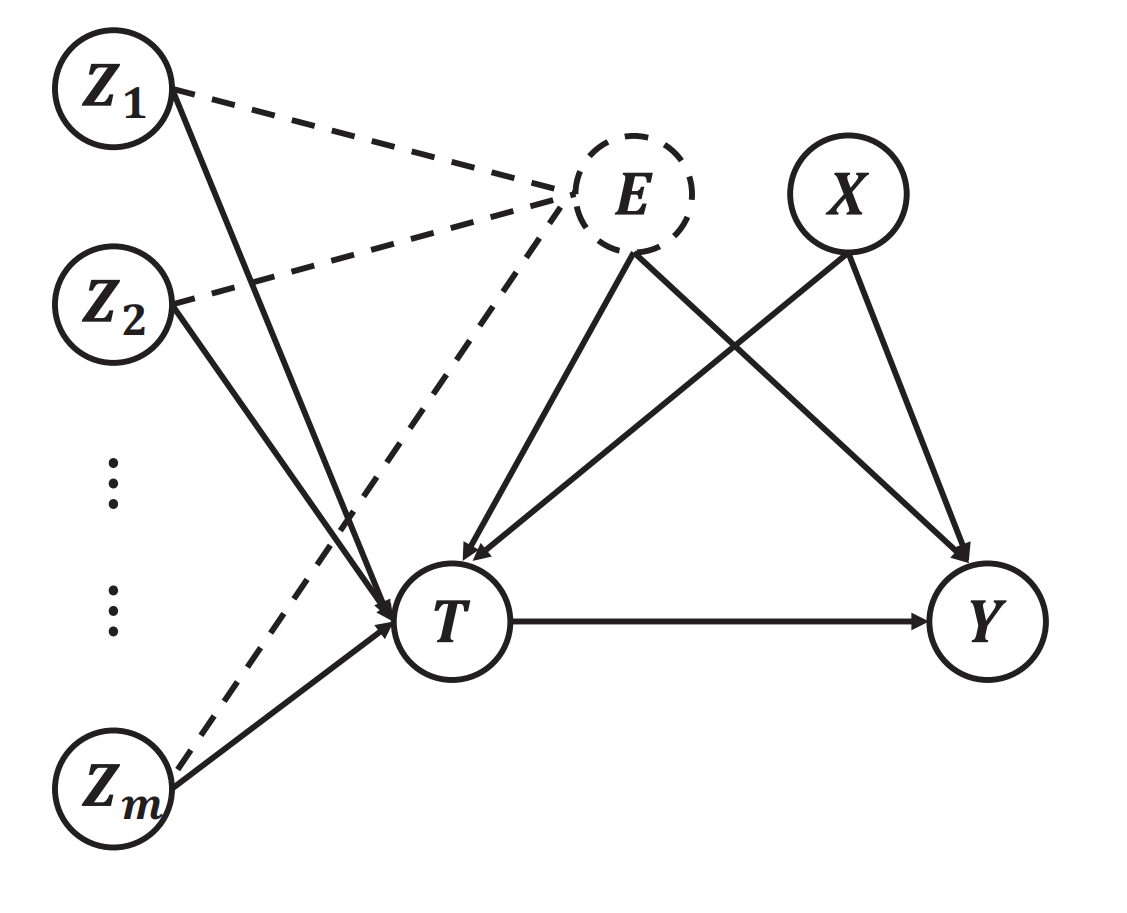
CVAE-IV方法[2]:传统工具变量(IV)回归方法依赖于预先定义好的IV,满足不受约束的工具假设(即给定观察到的协变量,IV与未测量的混杂因素独立),这是不可检验的,导致寻找有效的IV成为一门艺术而不是科学。为了解决该问题,我们提出了CVAE-IV方法,重点讨论了用违反非混杂工具假设的混杂工具估计个体因果效应的问题。通过考虑混杂工具集和结果变量之间的条件独立性,CVAE-IV方法利用用条件变分自动编码器生成未测量的混杂因素的替代。理论分析保证了生成的混杂因素替代物将识别无偏的个体因果效应。广泛实验也验证了该方法的有效性。
寻找有效的IV成为一门艺术而不是科学,通过机器学习赋能因果推断,我们研究了从复杂数据中找到或生成工具变量的挑战问题。为了实现该目标,分别提出了群体工具变量生成模型(GIV)[3]和工具表征自动生成(AutoIV)算法[4]。
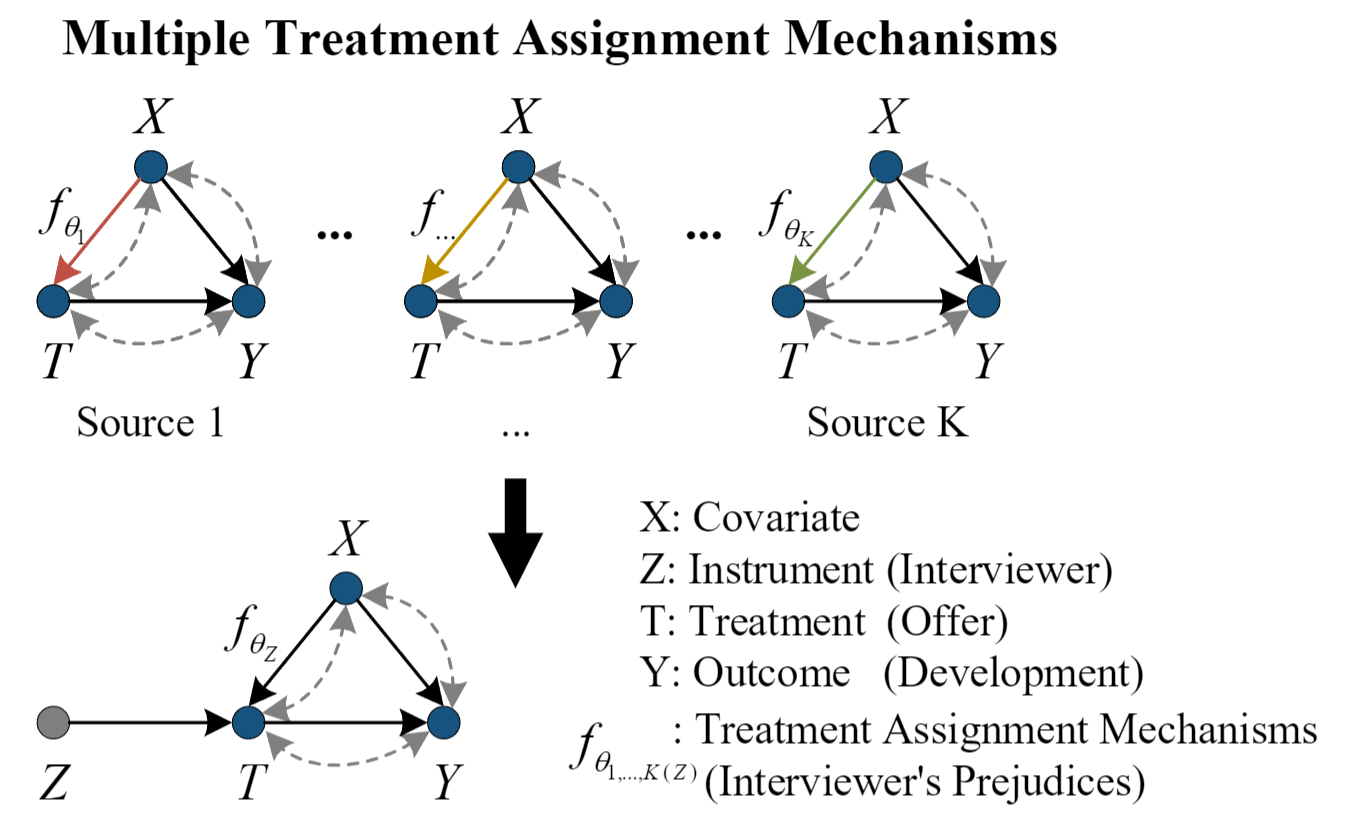
大数据时代的到来为在数据融合中得出干预效果带来了新的机遇和挑战,即需要从多个来源混合数据集(每个来源有独立的干预分配机制)中辨析干预变量。由于可能存在遗漏的源标签和未测量的混杂因素,传统方法无法估计个体干预分配概率并有效推断干预效果。因此,我们建议重构源标签,并将其作为一个群体工具变量(GIV)来实现基于IV的回归,以估计干预效果。为了实现群体工具变量的发现和生成,我们提出了一个统一的框架(Meta-EM)[3],以(1)将原始数据映射到一个表示空间中,为分配的干预变量构建线性混合模型;(2)估计分布差异,为不同的干预分配机制建立GIV模型;(3)采用交替训练策略,反复优化表示和联合分布,为IV回归的GIV建模。实证结果表明,与最先进的方法相比,Meta-EM具有明显优势。
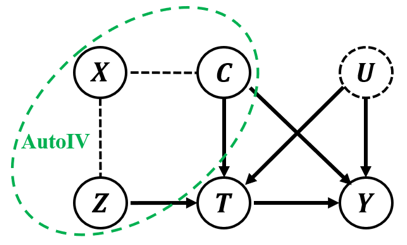
进一步,我们提出了工具表征自动生成(AutoIV)方法[4],从观察到的变量中自动生成工具变量的表征。AutoIV分别通过互信息最大化和最小化约束,让学习的工具变量表征满足与干预的相关和与结果的条件独立约束。实验表明,AutoIV可以生成有效的工具变量表征并准确地实现反事实预测和因果推断。
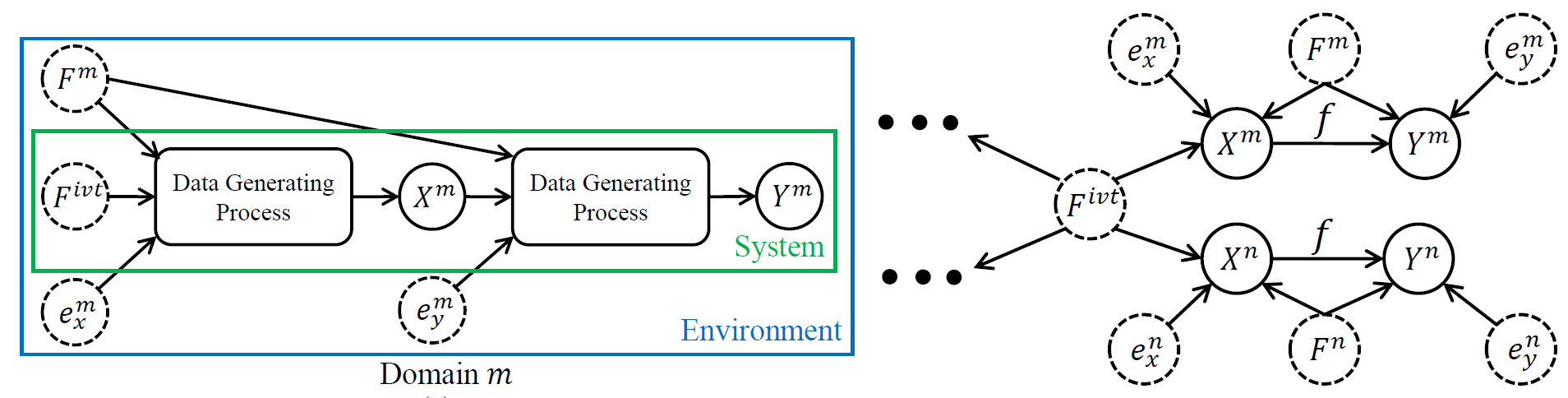
工具变量不仅是实现因果推断的有效方法,其亦可赋能机器学习,提升机器学习方法的可泛化性。机器学习中领域泛化问题旨在从多个源域学习一种能够在未知的目标域上较好泛化的模型。现有的方法主要学习输入特征的边缘分布不变的表征,然而,辨析输入特征下标签的条件分布不变性对于未知域泛化更为重要。同时,不可观察的混淆因素的存在会影响输入特征和标签的分布,导致虚假相关性,并阻碍对条件分布中包含的不变因果关系的学习。有趣的是,从数据生成过程的因果角度来观察,我们发现一个域的输入特征对其他域来说可以作为有效的工具变量。受这一发现的启发,我们提出了一种工具变量驱动的领域泛化方法(IV-DG)[5],通过两阶段学习消除未观察到的混淆因素的偏差。理论分析和实验表明,IV-DG方法产生了良好的域外泛化结果。
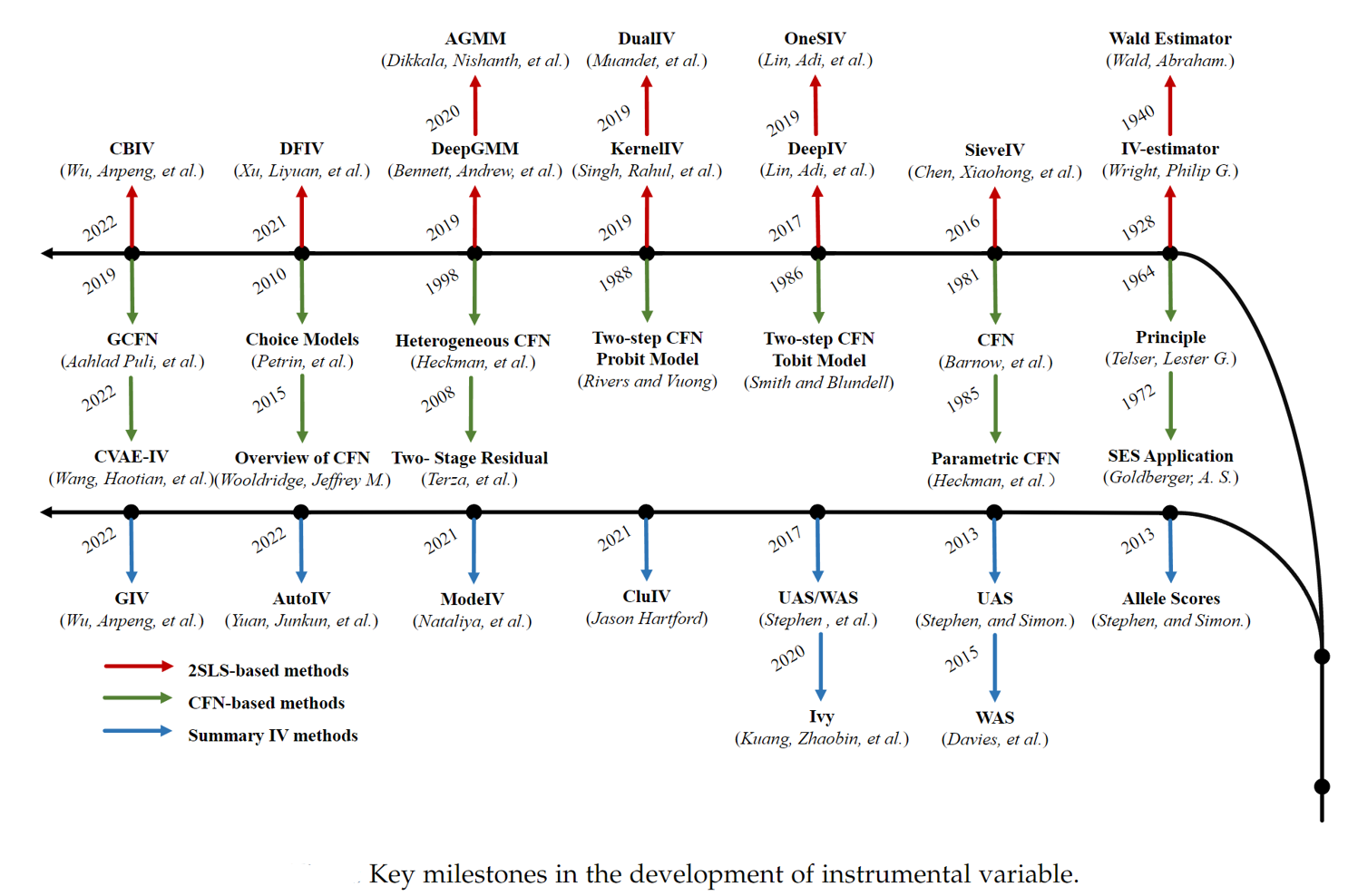
为了进一步促进因果推断和机器学习双向赋能,我们对因果推断和机器学习领域中工具变量相关方法进行了全面调研,并形成了一篇综述文章[6],分别从基于两阶段回归的方法、基于控制方程的方法以及基于工具变量生成的方法进行了全面介绍。同时开源开放了基于工具变量的大数据因果推断框架(MLIV,Machine Learning for Instrumental Variable,https://github.com/causal-machine-learning-lab/mliv)。
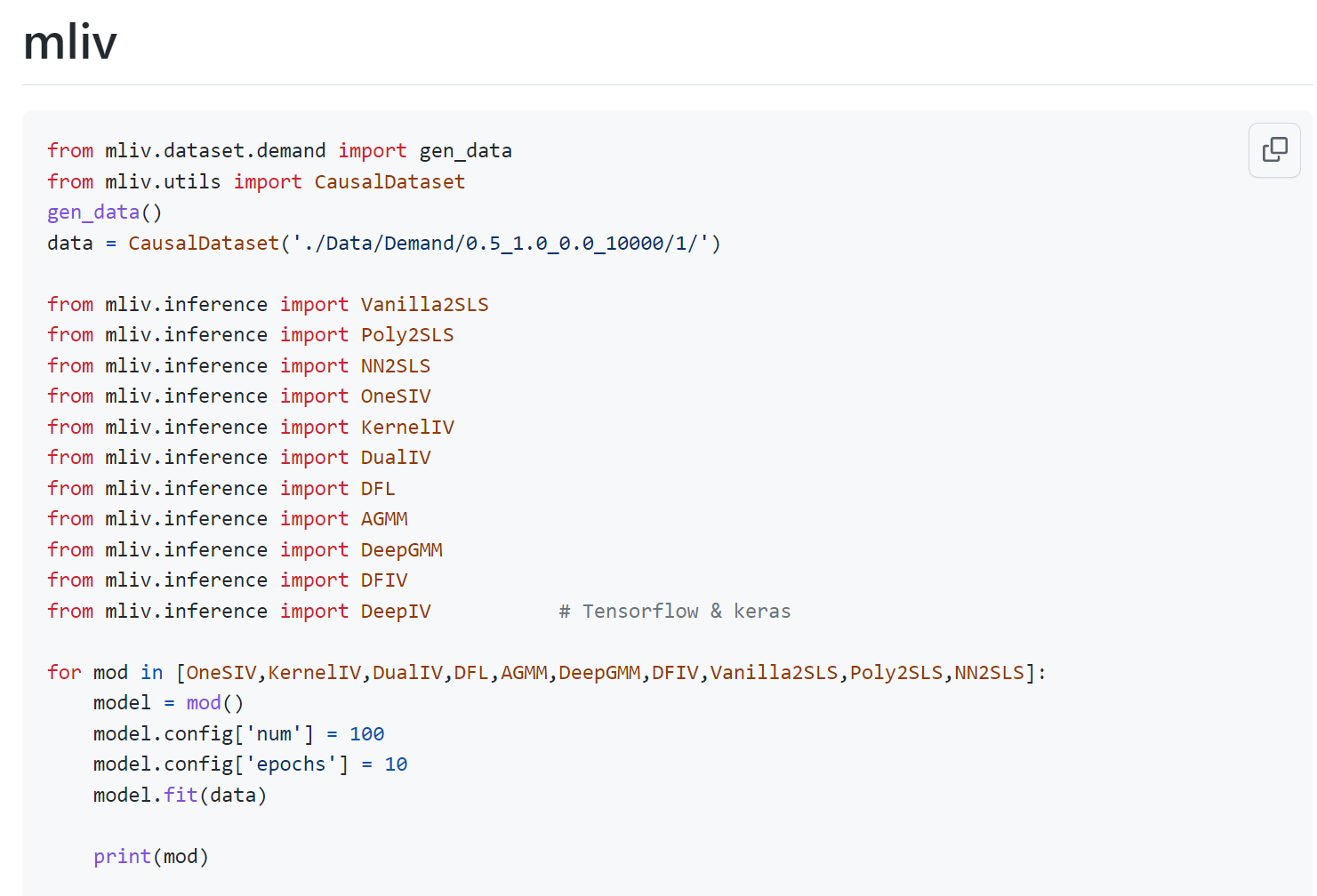
MLIV是一个基于工具变量进行因果推理的python包,实现了大量经典和前沿的工具变量算法。鉴于机器学习近来在各领域的大放异彩,MLIV着重实现了最新的使用机器学习进行工具变量学习的算法,并提供了一种标准数据格式和调用模式,允许用户根据实验数据或观测数据进行平均因果效应(ATE)估计或个体因果效应(ITE)估计,即条件平均因果效应(CATE)。此外,MLIV对模型没有任何强假设,并且不再依赖于因果推理中难以解决的非混淆性假设(Unconfoundedness),只要求数据中存在或足以构建一个有效的工具变量。
MLIV当前支持以下工具变量法:
IV Inference
2-Stage Least Squares (2SLS)
Vanilla2SLS
Poly2SLS
NN2SLS
Sieve Function
KernelIV
DualIV
Deep Learning
OneSIV
DeepIV
DFIV
Generalized Method of Moments (GMM)
AGMM
DeepGMM
IV Selection
Summary Method
UAS
WAS
ModeIV
Machine Learning
AutoIV
ClusterIV
MLIV还提供了工具变量法的Benchmark数据集-Demand数据集。
相关成果论文:
[1]. Anpeng Wu, Kun Kuang, Bo Li, Fei Wu. Instrumental Variable Regression with Confounder Balancing, ICML, 2022.
[2]. Haotian Wang, Wenjing Yang, Longqi Yang, Anpeng Wu, Liyang Xu, Jing Ren, Fei Wu, Kun Kuang. Estimating Individualized Causal Effect with Confounded Instruments, KDD, 2022.
[3]. Anpeng Wu, Kun Kuang, Ruoxuan Xiong, Minqin Zhu, Yuxuan Liu, Bo Li, Furui Liu, Zhihua Wang, Fei Wu. Learning Instrumental Variable from Data Fusion for Treatment Effect Estimation, AAAI, 2023.
[4]. Junkun Yuan, Anpeng Wu, Kun Kuang, Bo Li, Runze Wu, Fei Wu, and Lanfen Lin. Auto IV: Counterfactual Prediction via Automatic Instrumental Variable Decomposition, Transactions on Knowledge Discovery from Data (TKDD) , 2021.
[5]. Junkun Yuan, Xu Ma, Ruoxuan Xiong, Mingming Gong, Fei Wu, Lanfen Lin, Kun Kuang. Instrumental Variable-Driven Domain Generalization with Unobserved Confounders, TKDD, 2023.
[6]. Anpeng Wu, Kun Kuang, Ruoxuan Xiong, Fei Wu. Instrumental Variables in Causal Inference and Machine Learning: A Survey, https://arxiv.org/abs/2212.05778.


