Cavitation and fracture are both primary failure modes of soft materials, which could occur when pressure-sensitive adhesion layers subjected to tension or peeling tests. In recently years, cavitation and fracture gradually found themselves in emerging biomedical scenarios such as revealing the potential mechanism of traumatic brain injury caused by impact, and improving the effectiveness of high-intensity focused ultrasound treatment for diseases, thus research on soft materials cavitation under high-speed loading has gained increasing attention.
Bubble defects have significant impact on cavitation behavior. Professor Shaoxing Qu from Zhejiang University is specialized in mechanics of soft materials such as hydrogel, and he introduced size-controllable microbubble defects for impact experiments, and employed vibration model for single bubble to reveal how surface energy influence cavitation nucleation, to study critical defect size to control the dynamics of bubble. In addition, Professor Qu and his team further derived the weak interaction equations of multi-bubble vibration to predict deformation-inhibition behavior, and simulated the results to reveal the fusion mechanism.
Defects in soft materials expand rapidly in critical hydrostatic tension, leading to cavitation or rupture (Figure 1). The failure is determined by mechanical properties and defects sizes. The transition from cavitation to rupture in different failure modes in soft materials is yet to be fully understood. Recently, Professor Shaoxing Qu and his team combined the Griffith's fracture criterion and finite deformation theory to derive the critical initial size of defect for cavitation/rupture transition, namely the fractocohesive length Γ/Wf. They found that for highly stretchable soft materials, Γ/Wf can be orders of magnitude smaller than elasto-adhesive length Γ/E previously proposed.
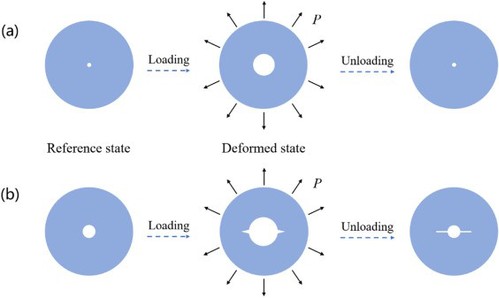
Figure 1. Schematics of two failure modes for soft materials with an initial defect in reference state: cavitation and fracture. (a) Cavitation: in deformed state, a small initial defect expands self-similarly under loading P, and recovers its original state when unloaded. The deformation process is elastic and may induce uniform damage around the cavity. (b) Fracture: in deformed state, a large initial defect expands to grow cracks on the internal surface of soft materials under loading P, and cracks cannot heal when unloaded. The deformation process is inelastic. The failure modes are related to the initial size of the defect in soft materials.
The authors first obtained the elastic modulus, fracture energy, and fracture toughness parameters of polyacrylamide hydrogel in thin film experiments. Hydrogel precursor was carefully poured into an acrylic mold, and illuminated under a UV lamp. Polyacrylamide hydrogels were demolded after curing for further mechanical tests. The researchers tested two hydrogel samples with different degree of crosslinking: sample 1, Γ/Wf=1.8mm, Γ/E=1.8mm; sample 2, Γ/Wf=1.7mm, Γ/E=19.4mm.
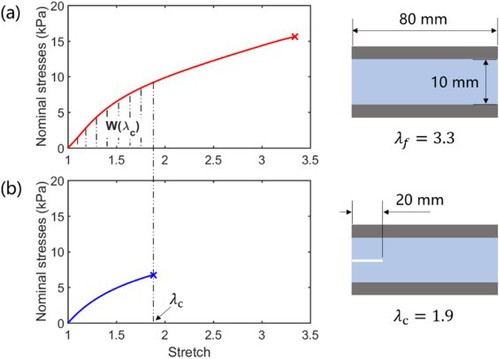
Fig. 2. Experimental measurement of toughness of polyacrylamide hydrogels from recipe 1. (a) A sheet sample without a precut has a length of L=80mm, height of H=10mm and thickness of T=2mm in its reference state. Upon loading, a nominal stress-stretch curve was recorded. Young's modulus E, strength sf, stretchability, and work of fracture can be obtained from this curve. The sample ruptures at a critical stretch. (b) A sheet sample with a precut of length 20mm has the same dimensions as the uncut one. Upon loading, a nominal stress-stretch curve is recorded. The stress is the force divided by the cross-sectional area without the precut, and the sample ruptures at a critical stretch. Toughness is calculated as the product of the energy density at critical stretch and the height H of the sample.
A cavitation rheology was set up to verify theoretical predictions, as show in Figure 3. The bottom of the cylindrical hydrogel sample (diameter 18mm, height 25mm) is fixed on a lifting platform. A sharp needle is inserted into the sample by adjusting the height of the lifting platform. The needle tip has an elliptical shape with long axis of rn, and considered to be far away from the boundary of the sample. Eight needles of different sizes are used in the experiments: rn = 0.6mm, 0.9mm, 1.3mm, 1.7mm, 2.2mm, 2.6mm, 3.8mm and 5mm. The testing machine pushes the plunger of a syringe fixed on the aluminum frame, injecting air into the hydrogel sample. The initial defect grows into a bubble. The pressure in the bubble is recorded by a pressure sensor, and the surface of the bubble is simultaneously captured by a camera. Failure mode is determined by the roughness of the bubble surface after the second process: a smooth bubble surface is considered as the cavitation mode, whereas a rough bubble surface is considered as the fracture mode.

Figure 3. Experimental setup of cavitation rheology.
To verify the cavitation/fracture transition size predictions of 1.8mm for recipe 1 and 1.7mm for recipe 2, researchers used eight needles with varying sizes. The results in Figure 4 showed that when the needle size is relatively small, the surface of the bubble is smooth; when the needle size increases to 2.6mm, the surface of the bubble begins to become rough, and the one corresponding to the needle size of 5mm becomes extremely rough. The roughness of the two bubbles around the fractocohesive length (1.8mm) is elusive. It can be judged from Figure 4(a) that when the needle size is 2.6mm, the bubble expansion is already caused by fracture. Similar phenomenon can be seen from Figure 4(b) for the samples made by recipe 2.

Figure 4. Experimental photos of bubbles with eight needle sizes after the second process. (a) Samples from recipe 1. (b) Samples from recipe 2. Red star on the arrow line indicates the fractocohesive length of the hydrogel, which is 1.8mm for recipe 1 and 1.7mm for recipe 2. For both recipes, bubble surface changes from smooth to rough when needle size is about 2.6mm.
Researchers examined the transition between cavitation and fracture in polyacrylamide hydrogels, using critical pressure to judge the expansion mechanism. They found that a nonlinear fitting equation Pf=αrnβ, provided better results, with fit values α=24.6 for recipe 1 and 16.9 for recipe 2; β=-0.24 for recipe 1 and -0.16 for recipe 2. The transition sizes were about 1.9mm and 1.8mm, which were close to the fractocohesive lengths of 1.8mm and 1.7mm. This indicates that the transition between cavitation and fracture in highly stretchable materials is controlled by the fractocohesive length (Γ/Wf) rather than the elasto-adhesive length (Γ/E). Further study is needed to understand the relationship between coefficients and material properties. For soft materials like elastomers and hydrogels with high toughness, the transition length should be controlled by Γ/Wf instead of Γ/E. This was supported by data from various studies, where Γ/Wf values are found to be in better agreement with experimental results than Γ/E values. This analysis suggested that the transition size between cavitation and fracture in soft materials takes the same form as that for metals.
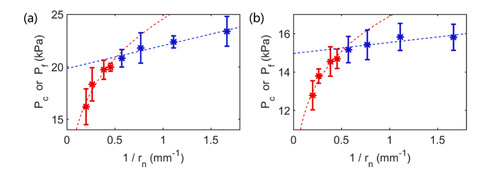
Figure 5. Critical pressure Pf for fracture as a function of the reciprocal of needle size 1/rn. (a) Data from recipe 1. (b) Data from recipe 2. Each data point is the average from ten samples, and error bar is the standard derivation. Dash lines are the fittings under different theoretical models. Black dash lines are fitted by krn−1/2, and red dash lines are fitted by αrnβ.
In summary, by considering the large deformation and nonlinear behavior of soft materials, the authors proposed that the cavitation-fracture transition size can be predicted by fractocohesive length Γ/Wf. This prediction is supported by the data on surface roughness and critical expansion pressure of bubbles in cavitation rheology tests. When the initial defect size is smaller than Γ/Wf, the sample fails by cavitation; when the initial defect size is larger than Γ/Wf, the sample fails by fracture. The value of fractocohesive length can be several orders of magnitude smaller than the elasto-adhesive length for highly stretchable materials, and these two length can be close for soft solids with highly degree of cross-linking. The results may shed light on a wide range of applications including trauma protection, biomedical therapy, material design and characterization, and so on.
The work was published as ‘Cavitation/fracture transition of soft materials’ in Journal of the Mechanics and Physics of Solids, and to access the article, please visit https://www.sciencedirect.com/science/article/pii/S0022509622003684.
About Professor Qu
Dr. Shaoxing Qu is a Changjiang Chair Professor (from Ministry of Education, China) and Distinguished Young Scholar grant from National Natural Science Foundation of China. He serves as the Director of the Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, and is currently an Adjunct Professor of Shanghai Institute for Advanced Study of Zhejiang University (SIAS).
He got his bachelor degree from University of Science and Technology of China in1997, Master of Engineering from Tsinghua University in 2000, and Ph.D. from UIUC in 2004. After spending two years at Brown University as postdoc, he joined Zhejiang University in 2006 and was promoted to full professor in 2011. He has published more than 180 journalpapers.
Dr. Qu’s primary research interests include soft materials and soft machines, insect-scalerobots, mechanics of composites, and micro/nano mechanics.
About SIAS
Shanghai Institute for Advanced Study of Zhejiang University (SIAS) is a jointly launched new institution of research and development by Shanghai Municipal Government and Zhejiang University in June, 2020. The platform represents an intersection of technology and economic development, serving as a market leading trail blazer to cultivate a novel community for innovation amongst enterprises.
SIAS is seeking top talents working on the frontiers of computational sciences who can envision and actualize a research program that will bring out new solutions to areas include, but not limited to, Artificial Intelligence, Computational Biology, Computational Engineering and Fintech.

